1 Introducción.

Una de las situaciones más comunes en investigación de ciencias médicas, es medir una variable numérica que se separa entre 2 o más grupos. Por ejemplo, en una investigación podría comparar cómo mejora la presión arterial entre pacientes sometidos a 2 tratamientos diferentes, o evaluar la producción una proteína en células expuestas a distintas dosis de un fármaco.

En estos casos, nos interesa saber si el promedio y/o la dispersión de la variable es diferente entre los grupos.

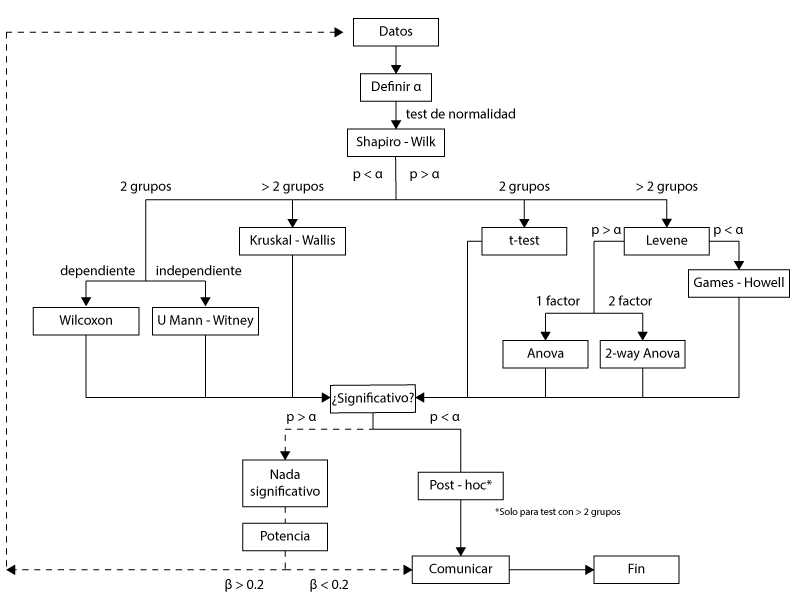
Figura 1. Algoritmo para escoger el test estadístico más adecuado cuando trabaja con variables numéricas.

Sin embargo, antes de hacer estas comparaciones necesitamos evaluar algunos aspectos de los datos, como su distribución, la cantidad de grupos o la dependencia de estos grupos. La figura 1 es el algoritmo para analizar datos cuantitativos, cuando éstos se separan en 2 o más grupos.

En este artículo nos centraremos en la distribución normal y la comparación de variables numéricas entre 2 grupos. En una siguiente entrada, continuaremos con los análisis que comparan variables numéricas ente más de grupos, y algunos aspectos de machine learning supervisado.

2 Distribución normal.

La distribución normal es la forma en que los datos se agrupan en la naturaleza, cuando han sido evaluados en forma aleatoria y, por lo tanto, representativa. Cuando los datos se ajustan a esta distribución, se le llama una muestra paramétrica.

Es fundamental evaluar si nuestros datos se ajustan a esta distribución, ya que muchos test estadísticos requieren que la muestra sea paramétrica. En caso que no se ajusten, podemos elegir un test no paramétrico, o bien, normalizar los datos.

Una forma sencilla de entender la distribución normal, es imaginar la estatura en una sala con 100 estudiantes. La mayoría de ellos tendrá una estatura promedio, por lo que podríamos agrupar una gran frecuencia de estudiantes que miden 1.70 m en el centro de la distribución. A medida que la estatura aumenta, la frecuencia de estudiantes va disminuyendo, de la misma forma que en las estaturas más bajas.

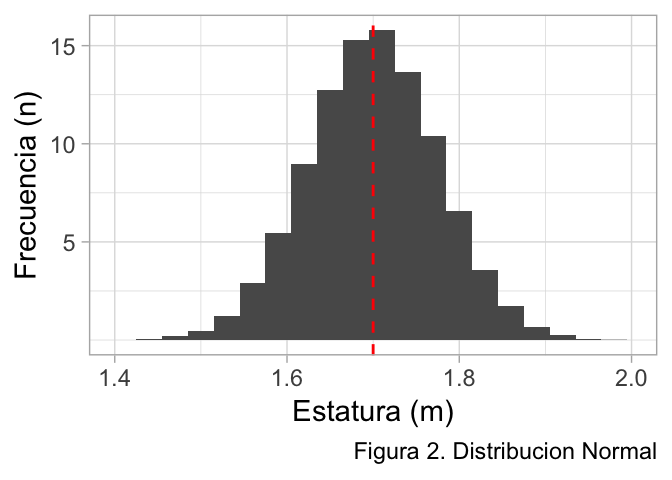
En la figura 2, podemos observar que la distribución normal tiene algunas características que la definen:

Una gran cantidad de datos agrupados al centro, y pocos en los extremos.
La línea roja muestra el promedio (1.70 m), y coincide con la mediana. Ergo, su forma es simétrica.
Debe tener un número mínimo para lograr su formarse, aproximadamente > 15 observaciones.

Para poder evaluar el ajuste de nuestros datos a la distribución normal, disponemos de muchas herramientas, por lo que nos centraremos en la visualización gráfica, el test de Shapiro Wilk, el test D’agostino Pearson Omnibus, y la representación gráfica de cuantil-cuantil.

2.1 Shapiro Wilk.

Para realizar este test, se calcula el promedio y la varianza de la muestra, y se ordenan todos los datos de menor a mayor. Luego, se compara la diferencia que existe entre el primero y el último, el segundo y el penúltimo. etc. De esta forma, análisis determina un estadístico W, que se extrapola a un p-value (1).

La hipótesis nula es que los datos se ajustan a la distribución normal, por lo que podemos asumir la normalidad de nuestros datos con un p-value mayor que alfa (p > 0.05).

2.2 D’agostino Pearson Omnibus.

El test de Shapiro Wilk es muy útil cuando el tamaño muestral es menor que 50, sin embargo, no es capaz de identificar la normalidad en muestras que superen este tamaño. Para resolver este problema, en el año 1971 se creó el test D’agostino Pearson Omnibus (2).

Este test estima un estadístico D, que se calcula a partir de la asimetría de la muestra y su curtosis.

Al igual que en Shapir-Wilk, el estadístico D se puede extrapolar a un p-value, que se interpreta de la misma forma (hipótesis nula es ajuste a la normalidad).

2.3 Gráfico cuantil-cuantil (Q-Q plot).

Finalmente, podemos evaluar la normalidad en forma visual con el Q-Q plot. Este gráfico compara los cuantiles de una muestra real con los cuantiles teóricos de una distribución de probabilidad.

Si recordamos, un cuantil es una división en partes iguales de un set de datos. Por ejemplo, si tenemos 100 observaciones entre 1.6 m y 1.8 m, los cuantiles teóricos se formarán dividiendo en 100 partes iguales el rango 1.6 - 1.8, obteniendo 100 cuantiles de 0.2 m en el eje Y. Estos cuantiles teóricos se comparan con las 100 observaciones reales en nuestro set de datos, obteniendo una correlación (fig 3).

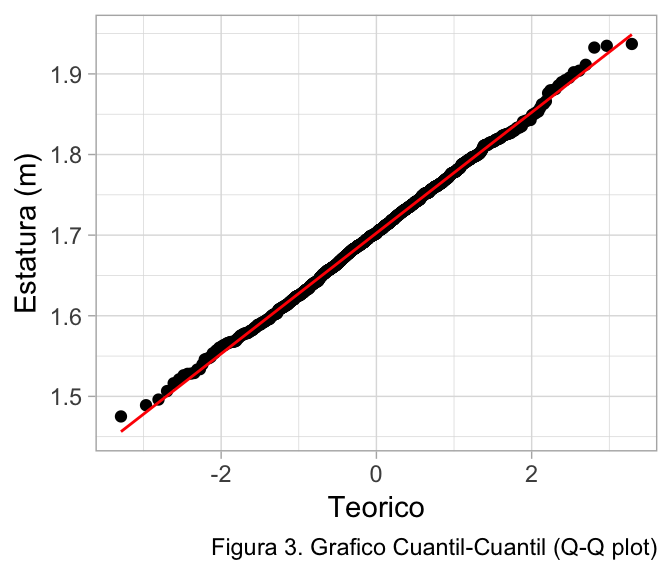
Si utilizamos R (recomendado), la función 'qqpnorm()' permite crear fácilmente este gráfico. En la figura 3, se han utilizado los mismos datos que en la figura 2, y se visualiza directamente como las observaciones (puntos) se ajustan a la curva teórica (línea roja), lo que sugiere normalidad.

3 Comparando 2 medias.

Una situación muy común en investigación, es medir una variable numérica separada en 2 grupos. Entonces, la estadística nos ayudará a responder si las diferencias que observamos en el promedio (o mediana) se deben al azar, o bien, si podemos extrapolarlas a la población.

En el ejemplo de la figura 4, se observan los resultados en la producción de insulina de cultivos de hepatocitos, que provienen de ratones hipertensos y controles (2 grupos).

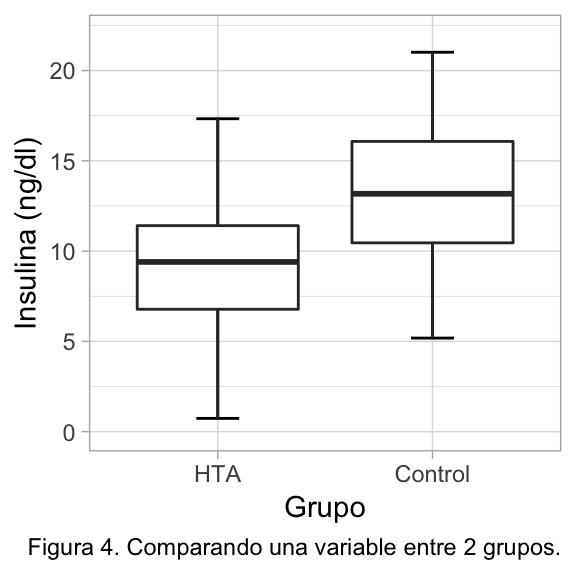
¿Producen más insluina los ratones controles? ¿Es significativa esa diferencia?

3.1 t-test independiente.

Permite identificar si el promedio y las desviaciones estándar de 2 grupos difieren significativamente.

Antes de realizar un t-test, se debe considerar si se cumple con los supuestos o assumptions (3):

Requiere que los grupos sean independientes, es decir, que una observación no dependa de otras observaciones. Esto se logra utilizando una correcta técnica de muestreo aleatorio.
La muestra debe ser paramétrica, es decir, debe obtenerse a partir de una distribución normal. Este assumption puede ser obviado cuando se trabaja con un tamaño muestral > 15 por grupo, ya que si realizamos un test no paramétrico llegaríamos a resultados extremadamente similares.
Igualdad de varianzas u homocedasticidad. Podemos evaluarlo de manera visual, o con el test de Levene, cuya H₀ es que las varianzas son homogéneas. Este test se aplica con la función 'leveneTest()' del paquete 'car'.

En R, podemos realizar el t-test con la función 't.test()', y si lo aplicamos al ejemplo anterior tendríamos el siguiente output:

## 
##  Two Sample t-test
## 
## data:  insulina by grupo
## t = -5.2633, df = 98, p-value = 8.349e-07
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -6.029237 -2.727593
## sample estimates:
##     mean in group HTA mean in group Control 
##              9.290493             13.668908

Podemos ver que el p-value es < 0.001, por lo que rechazaríamos la H₀. Además, podemos obtener resultados de interés clínico-fisiológico (tamaño del efecto), como el promedio de los grupos y el intervalo de confianza al 95% de la diferencia de medias.

3.2 t-test pareado.

Existen casos que el diseño experimental requiere que las muestras sean dependientes, entonces se puede optar por un t-test pareado o dependiente. Estos diseños nos permiten controlar muy bien las variables confundentes y covariables, al permitir emparejar uno o más factores entre los distintos grupos experimentales y controles.

Un ejemplo clásico es en estudios de odontología, donde se utiliza el diseño de “boca dividida”. Es este diseño, se divide la arcada dental sagitalmente en un lado derecho y otro izquierdo, exponiendo al paciente al tratamiento y control en cada lado. Es evidente que todos los factores se van a repetir entre los 2 lados, por lo que se considera que los grupos están pareados o son dependientes entre si.

Otros ejemplos son los Ensayos Clínicos Aleatorios de diseño cruzado, en que los mismos participantes del grupo experimental se intercambian al grupo control, o los estudios de cohorte emparejados por factores de riesgo. En el laboratorio también se realizan muchos diseños pareados, por ejemplo, si un cultivo celular separado a distintos tratamientos proviene de una misma fuente primaria, o en animales que son emparejados por ser de la misma camada.

En R, lo utilizamos agregando el argumento 'paired = True' a la función 't.test()'.

3.3 U Mann-Whitney – Wilcoxon test.

En los casos que no se cumpla el supuesto de normalidad, podemos reemplazar el t-test por el U Mann-Whitney en las muestras con observaciones independientes (4), o Wilcoxon para muestras pareadas (5).

Ambos test son muy simples de entender, básicamente ordenan todos los datos de ambos grupos en un ranking. Si los datos provienen de la misma población, se intercalarán los valores consecutivamente, ergo aceptaríamos la H₀. Si provienen de poblaciones distintas, los valores de los grupos quedarán separados, por lo que debería asumir que los grupos difieren significativamente, rechazando la H₀ (fig 5).

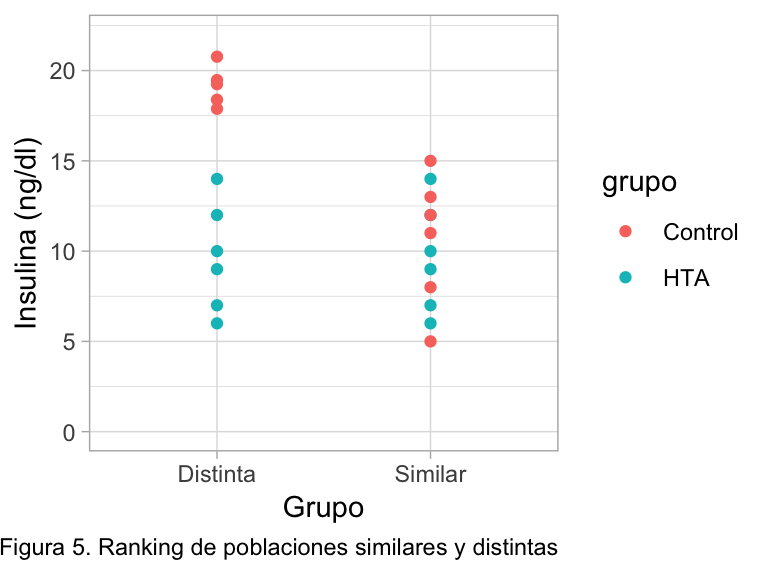
Ambos test se pueden aplicar en R con la función 'wilcox.test()', agregando el parámetro 'paired = TRUE' o 'paired = FALSE' para realizar el test U Mann-Whitney o Wilcoxon respectivamente.

Referencias

1. Shapiro SS, Wilk MB. An Analysis of Variance Test for Normality (Complete Samples). Biometrika. 1965 Dec;52(3/4):591–22.

2. D’Agostino RB. An Omnibus Test of Normality for Moderate and Large Size Samples. Biometrika. 1971 Aug;58(2):341–9.

3. Student. The Probable Error of a Mean. Biometrika. 1908 Mar;6(1):1.

4. Mann HB, Whitney DR. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. The Annals of Mathematical Statistics. 1947 Mar;18(1):50–60.

5. Wilcoxon F. Individual Comparisons by Ranking Methods. Biometrics Bulletin. 1945 Dec;1(6):80.

[Spanish] Análisis de variables numéricas, parte 1.